《高等数学》2.4 隐函数与参数方程求导

引入：

定义：\underset{隐函数}{F(x,y)}=0 \rightarrow \underset{显函数}{y=f(x)}

解：两边关于 x 求导（复合导数）

\begin{align*} \cos y \cdot y'+e^y\cdot y'-1&=0 \\ y'&=\dfrac{1}{\cos y+e^y} \\ y''&=\dfrac{\mathrm{d}}{\mathrm{d}x}\left(\dfrac{1}{\cos y+e^y}\right)\\ &=-\dfrac{-\sin y\cdot y'+e^y\cdot y'}{(\cos y+e^y)^2}\\ &=-\dfrac{-\sin y+e^y}{(\cos y+e^y)^3}\\ &=\dfrac{\sin y- e^y}{(\cos y+e^y)^3} \end{align*} \\

2. 求 \dfrac{x^2}{16}+\dfrac{y^2}{9}=1 在 (2,\dfrac{3\sqrt{3}}{2}) 的切线方程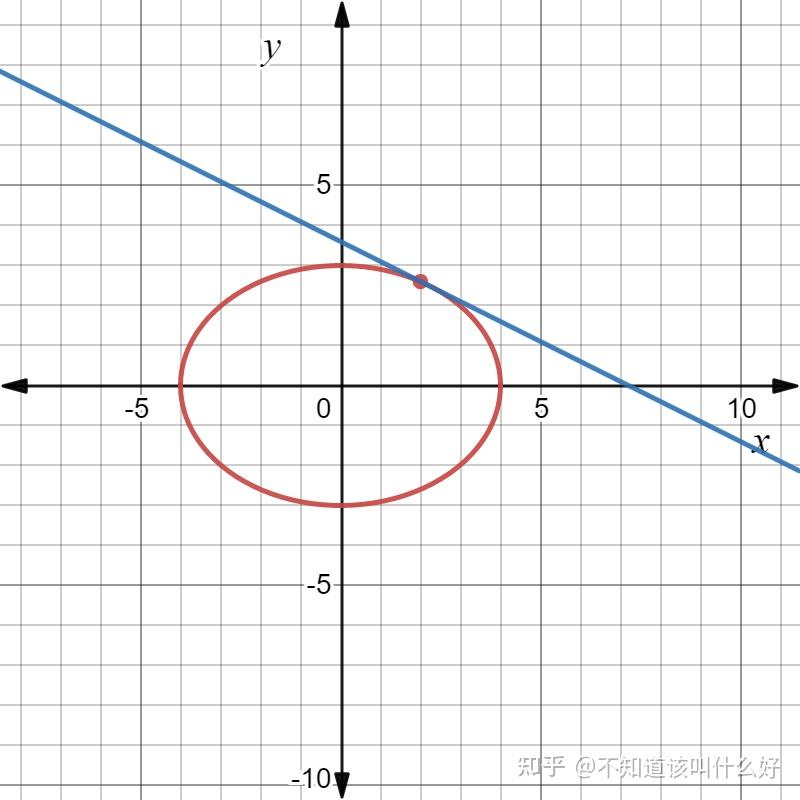

解：两边关于 x 求导

\begin{align*} \dfrac{2x}{16}+\dfrac{2}{9}y\cdot y'&=0\\ \dfrac{2}{16}\times 2+\dfrac{2}{9}\times \dfrac{3\sqrt{3}}{2}y'|_{x=2}&=0\\ k=y'|_{x=2}&=-\dfrac{\sqrt{3}}{4}\\ \therefore l:y-\dfrac{3\sqrt{3}}{2}&=-\dfrac{\sqrt{3}}{4}(x-2) \end{align*} \\

3. y=\left(\dfrac{a}{b}\right)^x\left(\dfrac{b}{x}\right)^a\left(\dfrac{x}{a}\right)^b,a\gt 0,b\gt 0,\dfrac{a}{b}=1，求 y'

解

法一：

\begin{align*} y'&=\left(\dfrac{a}{b}\right)^x\ln \left(\dfrac{a}{b}\right)\left(\dfrac{b}{x}\right)^a\left(\dfrac{x}{a}\right)^b+\left(\dfrac{a}{b}\right)^xa\left(\dfrac{b}{x}\right)^{a-1}\left(-\dfrac{b}{x^2}\right)\left(\dfrac{x}{a}\right)^b+\left(\dfrac{a}{b}\right)^x\left(\dfrac{b}{x}\right)^ab\left(\dfrac{x}{a}\right)^{b-1}\dfrac{1}{a}\\ &=a^{x-b}b^{a-x}x^{b-a}\ln\left(\dfrac{a}{b}\right)+a^{x+1-b}b^{a-x}x^{b-a-1}+a^{x-b}b^{a+1-x}x^{b-a-1} \end{align*} \\

法二（对数求导法）：

\begin{align*} \ln y&=x\ln(\dfrac{a}{b})+a\ln(\dfrac{b}{x})+b\ln(\dfrac{x}{a})\\ &=x\ln(\dfrac{a}{b})+a(\ln b-\ln x)+b(\ln x-\ln a) \end{align*} \\

\dfrac{1}{y}\cdot y'=\ln \dfrac{a}{b}-\dfrac{a}{x}+\dfrac{b}{x}

y'=y\cdot (\ln\dfrac{a}{b}+\dfrac{b-a}{x})=a^{x-b}b^{a-x}x^{b-a}(\ln \dfrac{a}{b}+\dfrac{b-a}{x})

y=f(x)\quad F(x,y)=0

解： \dfrac{\mathrm dy}{\mathrm dx}=\dfrac{2e^t}{-3e^{-t}}=-\dfrac{2}{3}e^{2t}

\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}=\dfrac{\mathrm d}{\mathrm dx}(-\dfrac{2}{3}e^{2t})=-\dfrac{4}{3}e^{2t}\cdot \dfrac{1}{-3e^{-t}}=\dfrac{4}{9}e^{3t}

2. \begin{cases}x=f'(t)\\y=tf'(t)-f(t)\end{cases} ，且 f^{(2)}(x)\ne 0 ，求 \dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}

解： \dfrac{\mathrm dy}{\mathrm dx}=\dfrac{f'(t)+tf''(t)-f'(t)}{f''(t)}=t

\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}=\dfrac{\dfrac{\mathrm d(\dfrac{\mathrm dy}{\mathrm dx})}{{\mathrm dt}}}{\dfrac{\mathrm dx}{\mathrm dt}}=\dfrac{1}{f^{(2)}(t)}

3. 求 r=e^{a\theta} 在 \theta=\dfrac{\pi}{2} 处的切线方程

解：

\begin{cases} x=\rho \cos \theta = e^{a\theta}\cos \theta\\ y=\rho \sin \theta = e^{a\theta}\sin \theta \end{cases} \\

k=\dfrac{\mathrm dy}{\mathrm dx}|_{\theta = \frac{\pi}{2}}=-a

l:y-e^{\frac{\pi a}{2}}=-ax 即 y+ax=e^{\frac{\pi a}{2}}

4. \begin{cases}x=t^2+2t\\t^2-y+\varepsilon \sin y=1\end{cases}(0\lt \varepsilon \lt 1)，求 y 对 x 的导数

解：

\dfrac{\mathrm dy}{\mathrm dx}=\dfrac{\frac{\mathrm dy}{\mathrm dt}}{\frac{\mathrm dx}{\mathrm dt}}=\dfrac{\frac{2t}{1-\varepsilon \cos y}}{2t+2}=\dfrac{t}{(1+t)(1-\varepsilon \cos y)}

设 x=x(t) 及 y=y(t) 都是可导函数，而变量 x 与 y 之间存在某种关系，从而变化率 \dfrac{\mathrm dx}{\mathrm dt} 与 \dfrac{\mathrm dy}{\mathrm dt} 间也存在一定关系。这两个相互依赖的变化率称为相关变化率。

解：

\dfrac{\frac{\mathrm dS}{\mathrm dt}}{\frac{\mathrm dr}{\mathrm dt}}=\dfrac{\mathrm dS}{\mathrm dr}=2\pi r

\dfrac{\mathrm dS}{\mathrm dt}|_{r=10}=2\pi \times 10 \times 2=40\pi (cm/s^2)

2. 圆锥形容器以 25cm^3/s 速度注水，当容器中的水位位于 \dfrac{h}{2} 时，求此时水位的上升速度。

解：

由相似关系得 \dfrac{r}{R}=\dfrac{h-x}{h}

\begin{align*} V&=\dfrac{1}{3}\pi R^2h-\dfrac{1}{3}\pi r^2(h-x)\\ &=\dfrac{1}{3}\pi R^2h-\dfrac{1}{3}\pi \left(\dfrac{R}{h}\right)^2(h-x)^3 \end{align*} \\

两边关于 t 求导得

\dfrac{\mathrm dV}{\mathrm dt}=0-\dfrac{1}{3}\pi \left(\dfrac{R}{h}\right)^2\cdot 3(h-x)^2\cdot (-1)\cdot \dfrac{\mathrm dx}{\mathrm dt}

\therefore \dfrac{\mathrm dx}{\mathrm dt}|_{x=\frac{h}{2}}=\dfrac{100}{\pi h^2}(cm/s^2)

查看更多高数笔记，请关注我的公众号文章列表

或知乎专栏地址